Scales
A scale is an ordered sequence of notes.
There have been various scales in use at different times and in different places.
Most, for historic reasons, are defined with ascending notes, but they can also descend!
Sometimes these two directions don't include the same notes.
Scales are the basis of melody.
They display the permitted notes and some of the rules of progression between them.
However, some sequences such as 20th century "note rows" are more of a silly affectation than proper scales.
Pentatonic Scale
The pentatonic scale is based on the simplest harmonic ratios and therefore is rediscovered by most cultures.
It is a five note or interval (tone) scale.
One way of generating it is to start at a fundamental or tonic note and go upwards in fifths (ratio 3:2).
This gives a sequence like C G D' A' E".
Collapse this into one octave to get C D E G A which will repeat at the octave C'.
Another way of generating it is to start with the major triad from the 3rd octave harmonic sequence, eg C E G.
Then add tones above the principle notes, C and G give D and A respectively, as in the 4th octave harmonics.
The black notes of a piano keyboard make a pentatonic scale.
It is not really a coincidence.
The 7-note scale of tones and semitones (from 12 semitones in total) forces 5 gaps that are tones and minor thirds apart - ie pentatonic.
This scale can be used in major or minor form, eg C D E G A C' or A C D E G A'.
It is the basis of many tunes around the world, eg Scotland, China, Japan, India, Africa and pre-conquest America.
The pentatonic scale pre-dates harmony.
If harmonies were to be added, there are only 2 possible triad chords.
The major triad, C E G, and the minor triad, A C E.
7-Note Scale
The modern European scale has 7 notes per octave.
The word octave refers to the 8 notes counted when both ends are included.
The natural way of generating it is to start with the major triad from the 3rd octave harmonic sequence, eg C E G.
Then add the triads to the fifths above and below, ie G B D and F A C.
Then collapse this, ie F A C E G B D, into one octave to get C D E F G A B.
The artificial way of generating it led to the system of tetrachords and modes (see below).
This latter way is the generally accepted method because it was written down at the time by a theoretician.
However, it was not immediately adopted by the general population.
Practical musicians almost certainly came to the same conclusion by more natural means.
| Triad Derivation |
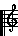 |
     |
   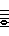  |
 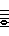    |
2.gif) |
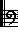 |
     |
     |
     |
8.gif) |
| FAC | CEG | GBD | |
|
| Ordered Scale |
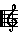 |  |
 |  |
 |  |
 |  |
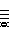 |  |
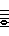 |  |
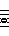 |  |
 |  |
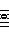 |  |
.gif) |
|
| |
| | |
| |
| |
| | |
| |
| |
| |
| | |
| |
| | |
c | | |
d | | |
e | | |
f | | |
g | | |
a | | |
b | | |
c | | |
| |
|
Tetrachords & Modes
It was Pythagoras, in about 550 BC, who investigated mathematics in music using strings.
He was the first to formally introduce the octave as the most important interval - though all these names came later.
He discovered it by dividing the string halfway (1/2 is the inverse of ratio 2:1).
The divisions at 2/3 and 3/4 the length gave him the perfect fifth and fourth (ratios 3:2 and 4:3).
The difference between these (1/12 of the whole string or 1/6 of the octave) he identified as a tone.
Pythagoras used this tone to divide up the larger intervals between fundamental & fourth and fifth & octave.
He found each required two tones and one half tone or semitone.
The total was then 7 intervals (3 on each side and 1 in the middle).
However, there were obviously 3 different arrangements of the divisions in each fourth.
He called them tetrachords (4 notes counting both ends).
The Lydian Tetrachord was tone-tone-semitone.
The Phrygian Tetrachord was tone-semitone-tone.
The Dorian Tetrachord was semitone-tone-tone.
Pythagorean Tetrachords & Modes
A scale or mode was made from one of these tetrachords followed by a tone and another tetrachord.
There are 9 possible arrangements but some of them put the semitones too close together or far apart to be usable.
The 5 remaining ones are consistent with each other since they use the same pattern shifted round like modula arithmetic.
The best possible spacing of semitones is unavoidably unequal and puts them fifths and fourths apart.
Pythagoras's original mode names used matching pairs of tetrachords.
In the 4th century, Bishop Ambrose chose 4 modes for church music (octaves starting on D, E, F and G).
For some reason he avoided the obvious C (major) and A (minor).
In the 6th century, Pope Gregory added 4 "plagal" modes starting on the dominant of the 4 "authentic" modes.
In the 16th century, the monk Glareanus added 4 more modes and reorganised things into pairs with a plagal mode below each authentic one.
Unfortunately he got the Pythagorean names wrong.
| Pattern | Pythagorean | 16th C. Mode | Keyboard Version |
| TTS T TTS | Lydian | Ionian / Hypolydian | C D E F G A B C |
| TTS T TST | (usable) | Mixolydian / Hypoionian | G A B C D E F G |
| TTS T STT | - | - / - | (G A B C D Eb F G or A B C# D E F G A) |
| TST T TTS | - | - / - | (C D Eb F G A B C or D E F G A B C# D) |
| TST T TST | Phrygian | Dorian / Hypomixolydian | D E F G A B C D |
| TST T STT | (usable) | Aeolian / Hypodorian | A B C D E F G A |
| STT T TTS | - | - / - | (C Db Eb F G A B C) |
| STT T TST | - | - / - | (D Eb F G A B C D or E F G A B C# D E) |
| STT T STT | Dorian | Phrygian / Hypoaeolian | E F G A B C D E |
| TTT S TTS | (illegal) | Lydian / - | F G A B C D E F |
| STT S TTT | (illegal) | - / Hypophrygian | B C D E F G A B |
Although scales can be played on the white notes starting from F and B they are not a tetrachord mode.
This is because there is no tone in the middle - F has an augmented fourth and B has a diminished fifth.
For some reason B was regarded as sinful note, so the dominant (fifth) of the mode starting on E was redefined as C!
Note that if there was any confusion over B and Bb the scale on F would indeed be the original Lydian mode of Pythagoras.
This may be merely a coincidence as the Phrygian and Dorian modes have just swapped places.
It isn't really a coincidence that the modes with 2 names form a pentatonic scale - C D E G A.
Banning the pair formed from B leaves the 5 which are most usable because of the perfect fourth and fifth a tone apart.
The semitone spacing forces the spacing of the 2 larger gaps between one usable root note and the next.
16th Century Modes
In actual perfomance, much fudging of the notes in modes took place, eg Bb for B and F# for F.
This was acknowledged practice but not initially written into the music.
As the use of harmony and counterpoint increased, accidentals were inserted and then keys took over from modes.
Whole-Tone / Hexatonic Scale
This is a play-thing or conceit of certain composers (eg Mozart and Debussy).
The octave is divided into six equal tones.
As there are no semitones, no note has more significance than any other.
This means that music written using it sounds rather vague.
There are only two combinations of notes for it (ignoring start position)
For example: C D E F# G# A# and F G A B C# D#.
Chromatic / Dodecaphonic / Semitone Scale
This uses all 12 equally spaced notes in an octave.
Therefore there is only one combination of notes, but it can have any starting note.
For example: C C# D D# E F F# G G# A A# B.
Modern Scales
The major scale comes straight from one of Pythagoras: TTS T TTS or C D E F G A B C'.
There are two minor scales.
The melodic minor scale shows the notes a melody might use and this depends on the direction.
So it is a bizarre mixture of TST T TTS ascending and TST T STT descending.
For example, A B C D E F# G# A' G F E D C B A.
The harmonic minor scale shows the notes a harmony would use and direction is irrelevant.
So it is the same up and down but has both minor 6th and major 7th leading to a 3-semitone gap between them.
Its pattern is TST T S3S, eg A B C D E F G# A'.
With 12 equal semitones, these scales can be played starting at any of 12 notes (7 white and 5 black on the piano).
That note became the key-note or key.
To keep to the pattern required accidentals - initially sharps (#) and flats (b) but later double-sharps (x) and double-flats(bb).
Accidentals became so numerous that key-signatures were invented to put the majority of them at the start of each staff instead.
However, each black note (and some white notes) could be considered as the sharp or flat of a white note.
For example, G# is "enharmonic" with Ab.
This led to duplications of key definitions.
Major Scales
Harmonic & Melodic Minor Scales
Ragas
Ragas are traditional Indian (Asian) scales.
The sanskrit word raga means "musical mood".
There are differences between Hindustani (northern) and Carnatic (southern) systems.
However, both are based on a 7-note system with variations on the relative pitch of some notes.
Unsurprisingly, the ratios 2:1 (octave on the tonic) and 3:2 (fifth / dominant) are recognised.
The basic notes are: sa, re, ga, ma, pa, dha, ni.
As well as collections of notes, the full raga system includes subsets of these (5 note minimum),
different ascending and descending orders of note use and rhythms/metres.
Interestingly, the sanskrit word tala for metre means "palm of the hand" as opposed to the foot of European metre.
Ignoring these additional complications there are 10 Hindustani and 72 Carnatic ragas.
Carnatic
In Carnatic ragas, the tonic (sa) and dominant (pa) do not vary but the "sub-dominant" (ma) has 2 options (M1 and M2).
The other notes have 3 options each (eg R1, R2 and R3).
Not all combinations are possible.
R1 can appear with any G, but R2 can only appear with G2 or G3 and R3 can only appear with G3.
D and N have the same pattern as R and G.
There is no restriction on M.
6 R-G pairs, 2 M options and 6 D-N pairs makes 6x2x6 = 72 combinations.
From the restrictions it is reasonable to infer that there is some overlap or closeness of pitch between R & G and D & N options.
The actual notes won't be the same as European ones, but an approximation might be:
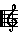 |
   |
   |
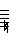   |
   |
 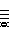  |
   |
   |
   |
 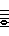  |
 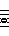  |
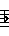   |
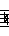   |
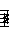   |
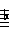 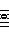  |
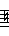 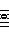  |
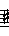 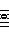  |
  .gif) |
| S |
R1 | R2 | R3 |
G1 | G2 | G3 |
M1 | M2 | P |
D1 | D2 | D3 |
N1 | N2 | N3 |
S |
In the lists I've seen, this guess is made more likely by the presence of pentatonic scales in the 5-note subsets when translated.
An alternative notation uses different vowel sounds in the syllables for the various alternatives.
So [ra, ri, ru], [ga, gi, gu], [ma, mi], [dha, dhi, dhu] and [na, ni, nu].
Hindustani
In Hindustani ragas, the tonic (sa) and dominant (pa) do not vary but the other notes have 2 options each.
There is no overlap, but only 10 basic combinations are used (out of a possible 32).
In one notation, the lower option is shown in lower case and the upper option is shown in upper case.
So a chromatic scale would be: S r R g G m M P d D n N.
However, the natural ma option is the lower one while the upper is considered sharp.
Whereas for the other 4 notes, the natural option is the upper one while the lower is considered flat.
A notation that reflects this uses a line above (sharp) or below (flat) the base note letter.
So a chromatic scale would be: S R R G G M M P D D N N (within the limits of HTML!).
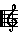 |
   |
   |
   |
   |
   |
   |
   |
 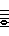  |
 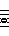  |
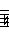 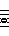  |
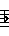   |
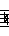   |
 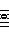 .gif) |
| S |
r | R |
g | G |
m | M | P |
d | D |
n | N |
S |
The 10 basic thaats are:
- SRGMPDN = Kalyan (= F "major" mode; ie sharp 4th)
- SRGmPDN = Bilaval (= C major mode)
- SRGmPDn = Khammaj (= G "major" mode; ie flat 7th)
- SRgmPDn = Kafi (= D "minor" mode; ie flat 3rd and 7th)
- SRgmPdn = Asavari (= A "minor" mode; ie flat 3rd, 6th and 7th)
- SrgmPdn = Bhairavi (= E "minor" mode; ie flat 2nd, 3rd, 6th and 7th)
- SrGmPdN = Bhairava (flat 2nd and 6th, like a pair of harmonic minor tetrachords)
- SrGMPDN = Marava (flat 2nd but sharp 4th)
- SrGMPdN = Pooravi (flat 2nd and 6th but sharp 4th)
- SrgMPdN = Todi (flat 2nd, 3rd and 6th but sharp 4th)
© Susan Foord
(sf@pedag.org)
2010-06-24
Linkage: | Home | Music Index |










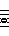


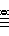

2.gif)
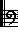

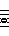


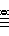










8.gif)
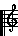










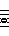


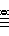

2.gif)
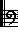

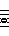


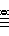










8.gif)
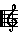









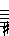






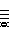


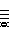


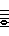

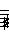
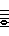


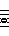

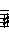
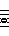





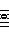

.gif)
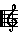






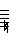













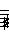
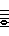


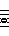

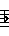


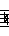


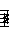


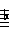
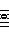

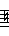
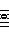

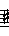
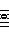



.gif)





















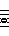

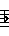


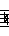



.gif)